Copyright © 2000-2011 Yves MARCOUX; dernière modification de cette page: 2011-09-20
Voir aussi l’exerciseur de diagrammes de Venn.
Les arbres renversés et les diagrammes de Venn sont des outils visuels qui aident à comprendre comment sont exécutées les requêtes complexes, c’est-à-dire comportant plus de deux termes et plus d’un opérateur.
Exemple d’une requête complexe:
(chien OU chat) OU furet
Cette requête contient trois termes de recherche et deux opérateurs (deux OU booléens).
La troncature * et le masque ? qui pourraient se trouver dans les termes de recherche ne sont pas comptés. Ainsi, par exemple,
chat* ET chien
n’est pas une requête complexe.
Même si les arbres renversés et les diagrammes de Venn sont surtout utiles pour représenter des requêtes complexes, ils peuvent aussi être utilisés pour représenter des requêtes simples (non complexes), c’est-à-dire comportant seulement deux termes de recherche et un opérateur.
Ce sont des outils qu’on a intérêt à utiliser surtout pendant qu’on se familiarise avec la recherche d’information; cependant, même les chercheurs expérimentés y reviennent parfois, soit pour mieux visualiser une requête particulièrement complexe, soit pour bien comprendre le fonctionnement d’un nouvel outil de recherche.
Le but d’un arbre renversé est de mettre en évidence l’ordre d’exécution des opérateurs dans une requête. Montrons d’abord un exemple, que nous commenterons ensuite. Il est à noter que ADJ est un opérateur d’adjacence qui repèrera les deux termes seulement s’ils sont l’un à côté de l’autre, dans le même ordre. La requête:
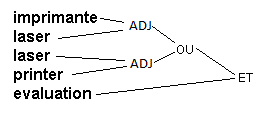
((imprimante ADJ laser) OU (laser ADJ printer)) ET evaluation
est représentée par l’arbre renversé suivant:

Un arbre renversé est constitué d’un certain nombre de colonnes, chacune comportant un ou plusieurs éléments « empilés » l’un au-dessus de l’autre. Dans notre exemple, l’arbre a quatre colonnes: la première (celle de gauche), comporte cinq éléments empilés, la deuxième, deux éléments, et les troisième et quatrième comportent chacune un élément.
Notons tout de suite que les éléments qu’on retrouve dans l’arbre sont les termes et les opérateurs de la requête. Ceux-ci apparaissent tels quels dans l’arbre, sauf les opérateurs, qui sont toujours représentés explicitement, et par leur nom en français pour les opérateurs booléens: ET, OU, SAUF.
En plus des termes et des opérateurs de la requête, on retrouve également des lignes qui relient certains éléments entre eux. Ces lignes indiquent quels termes ou autres résultats chaque opérateur relie. Ainsi, dans notre exemple, le premier ADJ (celui du haut dans la deuxième colonne) s’applique au terme imprimante et au premier des deux laser; le OU s’applique aux résultats des deux ADJ; le ET relie le terme evaluation et le résultat de l’évaluation du OU; etc.
L’ordre d’exécution des opérateurs correspond donc à leur ordre d’apparition dans l’arbre: les opérateurs dans la deuxième colonne s’exécutent avant ceux de la troisième, ceux de la troisième avant ceux de la quatrième, etc. L’ordre d’exécution des opérateurs à l’intérieur d’une même colonne n’a pas d’importance, car ces opérateurs sont indépendants l’un de l’autre (le résultat de l’un ne peut pas influencer le résultat d’un autre).
L’arbre renversé de notre exemple nous montre que le système va exécuter notre requête comme suit. D’abord, il va constituer deux ensembles de documents: ceux contenant imprimante laser, et ceux contenant laser printer. Ces deux ensembles correspondent aux deux ADJ de la deuxième colonne. Ensuite, il va fusionner (faire l’union de) ces deux ensembles avec le OU booléen (troisième colonne), ce qui va donner un troisième ensemble de documents: ceux contenant soit imprimante laser, soit laser printer (soit les deux). Finalement, le système va évaluer le ET booléen (quatrième colonne), c’est-à-dire faire l’intersection entre ce troisième ensemble et l’ensemble des documents contenant evaluation. Ce sera le résultat final de la requête.
Si cette interprétation est trop complexe, laissez-la de côté pour le moment, et revenez-y après avoir fait la section sur les diagrammes de Venn. Une bonne compréhension des opérateurs booléens vous aidera à comprendre les requêtes complexes en général, même celles qui incluent des opérateurs autres que les opérateurs booléens.
Voici maintenant les règles de construction de l’arbre renversé d’une requête, de façon un peu plus systématique:
La racine de l’arbre est l’opérateur situé sur la dernière colonne (celle de droite). Le résultat de cet opérateur est le résultat de la requête comme telle.
Pour déterminer à quoi s’applique chaque opérateur, il faut tenir compte des parenthèses, comme en arithmétique simple. Ainsi, dans la requête:
chien ET (chat OU furet)
le OU entre chat et furet s’applique à ces deux termes, alors que le ET s’applique à chien et au résultat du OU. Cette requête se traduit donc en l’arbre renversé suivant:
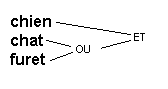
L’usage des parenthèses est conseillé lorsque l’ordre d’exécution des opérateurs n’est pas connu ou diffère de l’ordre que vous voudriez pour une requête. Si vous ne connaissez pas l’ordre d’exécution des opérateurs pour une requête complexe sans parenthèses, il ne vous sera pas possible d’obtenir un arbre renversé unique. Ainsi, la requête:
chien OU chat ET furet
peut être interprétée de deux manières différentes:
Il y aurait en ce cas deux arbres renversés possibles:
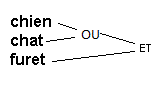
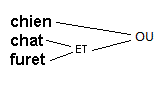
Ces deux interprétations possibles de la requête donnent des résultats différents. Il est ainsi important d’utiliser les parenthèses, au besoin, pour s’assurer que l’interprétation du logiciel correspond à l’interprétation désirée.
Exercice 1: Construisez l’arbre renversé correspondant à la requête:
(chien SAUF loir) OU (chat ADJ cheval)
Réponse:
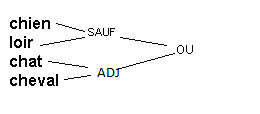
Exercice 2: Traduisez en arbre renversé la requête suivante (à noter: 2M est un opérateur de distance qui repére les deux termes avec un maximum de 2 mots qui les séparent, dans l’ordre ou dans le désordre):
(chien 2M loir) ET (chat OU cheval)
Réponse:
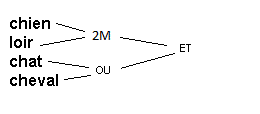
Exercice 3: Traduisez en arbre renversé la requête suivante:
((chien 2M loir) ET chat) OU cheval
Réponse:
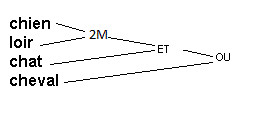
Un diagramme de Venn à deux termes est constitué de deux cercles entrelacés. À côté de chaque cercle est inscrit un terme qui lui est associé. Chaque cercle représente l’ensemble des documents qui contiennent le terme associé. Par exemple, ci-dessous, le cercle étiqueté « chien » représente l’ensemble des documents qui contiennent le mot « chien » et celui étiqueté « chat » représente l’ensemble des documents qui contiennent le mot « chat »:
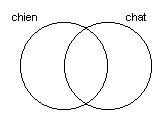
Les deux cercles délimitent trois régions du plan (quatre, si on compte celle à l’extérieur des cercles, mais nous ne la compterons pas pour le moment). Si on les numérote 1, 2 et 3 de gauche à droite, alors la région 1 représente l’ensemble des documents qui contiennent « chien » sans contenir « chat », la région 2 représente l’ensemble des documents qui contiennent à la fois « chien » et « chat », et la région 3 représente l’ensemble des documents qui contiennent « chat » sans contenir « chien »:
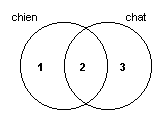
Évidemment, dans une base de données spécifique ayant un contenu spécifique, il se pourrait que l’une ou l’autre de ces régions ne contienne aucun document. Mais un diagramme de Venn représente le résultat d’une requête indépendamment d’une base spécifique sur laquelle on pourrait la faire exécuter. On tient donc compte de toutes les régions, puisque chacune a le potentiel de contenir des documents.
« Représenter une requête » à l’aide d’un diagramme de Venn veut dire colorer la ou les régions correspondant aux documents repêchés par la requête. Par exemple, la requête:
chien ET chat
se représente comme suit:
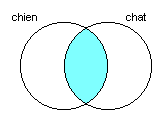
parce que cette requête repêche exactement les documents qui contiennent à la fois « chien » et « chat ».
Pour montrer qu’un certain diagramme correspond à une certaine requête, on inscrit la requête sous le diagramme:
 |
| chien ET chat |
Voici les diagrammes correspondant à deux autres requêtes:
|
|
Exercice 4: Dessinez le diagramme correspondant à la requête « chat SAUF chien ».
Réponse:
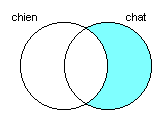
Les requêtes ci-dessus sont des requêtes simples (c’est-à-dire non complexes): elles ne comportent que deux termes et un opérateur. Représenter des requêtes simples par un diagramme de Venn est facile. Ce n’est pas toujours aussi facile pour des requêtes complexes. La méthode que nous allons maintenant voir permet de représenter sous forme de diagramme de Venn n’importe quelle requête booléenne complexe contenant deux termes distincts. Nous allons travailler avec un exemple, la requête:
(chien OU chat) SAUF (chien ET chat)
Les deux termes distincts de la requête sont chien et chat, nous travaillerons donc avec des diagrammes de la forme:

La première étape est de construire l’arbre renversé correspondant à la requête. Pour notre exemple, l’arbre renversé est:
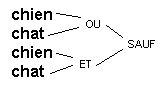
L’idée de ce qui suit est simple: nous allons associer un diagramme de Venn à chaque terme ou opérateur de l’arbre. Le diagramme que nous associerons à la racine de l’arbre sera celui qui représente la requête comme telle. Nous commençons par les termes (colonne de gauche), puis nous traitons ensuite les opérateurs, colonne par colonne, de gauche à droite, jusqu’à ce que nous arrivions à la racine.
La règle pour traiter les termes est extrêmement simple: à chaque terme est associé le diagramme dans lequel le cercle correspondant au terme est entièrement coloré. On inscrit le terme lui-même comme requête, sous le diagramme.
Donc, à la colonne de termes de notre exemple, sont associés les diagrammes suivants:
|
|
|
|
Nous sommes maintenant prêts à traiter les opérateurs. Tel que mentionné plus haut, nous allons procéder colonne par colonne, de gauche à droite. Chaque opérateur se verra associer un diagramme qui dépend du diagramme associé à chacun des deux éléments (terme ou opérateur) reliés par l’opérateur.
La façon de construire le diagramme associé à un opérateur varie selon qu’il s’agit d’un ET, d’un OU ou d’un SAUF. Voici les règles pour chaque type d’opérateur (dans ces règles, A et B représentent les diagrammes associés aux deux éléments que l’opérateur relie):
Ces règles peuvent sembler compliquées à première vue, mais elles ne font en fait que traduire des évidences, du genre: un document qui satisfait à la fois le critère A et le critère B satisfait aussi, par le fait même, le critère A ET B.
La poursuite de notre exemple devrait clarifier les choses. Nous en étions à traiter le ET et le OU de la première colonne d’opérateurs. Voici ce que nous obtenons en suivant les règles ci-dessus:
|
|
Nous arrivons finalement à la racine de l’arbre, l’opérateur SAUF. Nous appliquons donc la règle du SAUF, et nous obtenons:
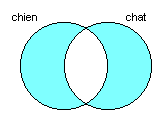 |
| (chien OU chat) SAUF (chien ET chat) |
Puisque nous sommes rendus à la racine de l’arbre renversé, c’est ce diagramme qui représente la requête comme telle. On voit bien, grâce à ce diagramme, que la requête repêche les documents qui contiennent soit « chien », soit « chat », mais pas les deux.
Exercice 5: Dessinez le diagramme de Venn correspondant à la requête:
(chien SAUF chat) OU (chat SAUF chien)
Réponse:

Exercice 6: Dessinez le diagramme de Venn correspondant à la requête:
chien ET (chat SAUF chien)
Réponse:

Exercice 7: Dessinez le diagramme de Venn correspondant à la requête:
chien OU (chat SAUF chien)
Réponse:
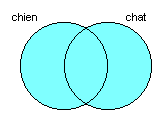
Le diagramme de Venn à trois termes est une généralisation de celui à deux termes. Il s’agit de trois cercles entrelacés, avec chacun un terme associé. Il permet de représenter le résultat de requêtes booléennes contenant trois termes distincts (chacun pouvant par ailleurs apparaître plusieurs fois). Voici un diagramme de Venn à trois termes:
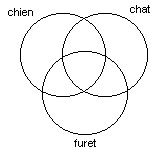
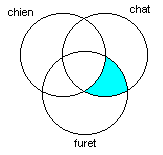
Un diagramme de Venn à trois termes délimite sept régions (sans compter celle à l’extérieur des cercles), qui correspondent à des ensembles de documents contenant différentes combinaisons des trois termes figurant dans le diagramme. Par exemple, la région colorée ci-dessous correspond aux documents qui contiennent « chat » et « furet », sans contenir « chien »:
On se sert des diagrammes à trois termes exactement comme des diagrammes à deux termes. Nous pouvons donc tout de suite y aller avec un exemple.
On veut dessiner le diagramme de Venn qui correspond à la requête suivante:
(chien OU chat) ET furet
La requête compte trois termes distincts: chien, chat et furet; nous travaillerons donc avec des diagrammes à trois termes, de la forme:

L’arbre renversé correspondant à la requête est:

Associés à la colonne de termes, nous avons donc les trois diagrammes suivants:
|
|
|
On poursuit avec l’opérateur OU:
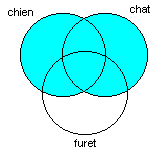 |
| (chien chat) |
On conclut avec le ET, qui correspond à la racine de l’arbre, pour lequel on obtient:
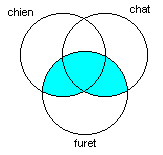 |
| (chien OU chat) ET furet |
Puisque nous sommes rendus à la racine de l’arbre renversé, c’est ce diagramme qui représente la requête comme telle.
Exercice 8: Trouvez le diagramme de Venn correspondant à la requête suivante:
chien OU (chat ET furet)
Réponse:
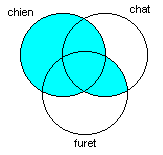
Exercice 9: Trouvez le diagramme de Venn correspondant à la requête suivante:
(begonia SAUF (tulip* OU pense*)) OU ((begonia ET tulip*) ET pense*)
Réponse:
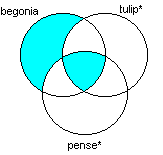
Exercice 10: Trouvez le diagramme de Venn correspondant à la requête suivante:
begonia SAUF ((tulip* OU pense*) SAUF ((begonia ET tulip*) ET pense*))
Réponse:

Exercice 11: Trouvez une requête qui correspond au diagramme de Venn suivant:
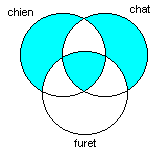
Notez qu’il y a plusieurs bonnes réponses.
Réponse: Nous allons décrire et appliquer une méthode générale pour solutionner ce genre de problèmes. Il s’agit de composer une expression pour chaque région colorée du diagramme, et de lier les expressions ainsi obtenues par des "OU" booléens.
Le diagramme donné comporte trois régions colorées:
|
|
|
Dans l’ordre, ces trois régions correspondent aux expressions suivantes:
chien SAUF (chat OU furet)
chat SAUF (chien OU furet)
chien ET chat ET furet
Il suffit de lier ces trois expressions par deux "OU" booléens pour obtenir la requête recherchée:
(chien SAUF (chat OU furet)) OU (chat SAUF (chien OU furet)) OU (chien ET chat ET furet)
On dit que deux requêtes sont équivalentes si elles donnent toujours le même résultat, peu importe le contenu de la base de données sur laquelle on les fait exécuter. Pour les requêtes booléennes (c’est-à-dire ne contenant que des opérateurs booléens) à deux ou trois termes distincts, cela revient à dire qu’elles correspondent au même diagramme de Venn (avec les mêmes termes aux mêmes endroits).
Par exemple, les requêtes chien SAUF chat et chien SAUF (chat ET chien) sont équivalentes; en effet, elles correspondent toutes deux au diagramme:
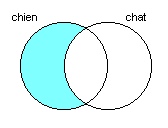
Exercice 12: Lesquelles, parmi les requêtes des exercices précédents, sont équivalentes?
Réponse: Il s’agit de trouver les requêtes qui correspondent au même diagramme de Venn (avec les mêmes termes aux mêmes endroits). Il n’y a que les requêtes des exercices 9 et 10 qui sont dans ce cas; ce sont donc les deux seules requêtes équivalentes.
Exercice 13: Trouvez le diagramme de Venn correspondant à la requête suivante:
chien ET (chat OU furet)
Réponse:
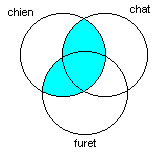
Exercice 14: Trouvez le diagramme de Venn correspondant à la requête suivante:
chien OU (chat OU furet)
Réponse:
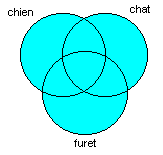
Exercice 15: Trouvez le diagramme de Venn correspondant à la requête suivante:
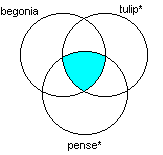
begonia ET tulip* ET pense*
Réponse:
Encore plus d’exercices du même genre? Essayez l’exerciseur de diagrammes de Venn.
Les exercices suivants consistent tous à trouver une requête qui correspond au diagramme de Venn donné. Dans tous les cas, il y a plusieurs réponses possibles; nous n’en donnons qu’une, mais il existe d’autres bonnes réponses. Pour l’Exercice 19, nous donnons également une « preuve », c’est-à-dire la reconstruction du diagramme de Venn à partir de la requête donnée en réponse.
Une méthode générale pour solutionner ce genre de problèmes est présentée ci-dessus à l’Exercice 11.
Rép.: ((coussin OU table) SAUF divan) SAUF (coussin ET table)
Rép.: ((coussin OU divan) SAUF table) OU (coussin ET divan ET table)
Rép.: ((coussin ET divan) OU (divan ET table) OU (table ET coussin)) SAUF (coussin ET divan ET table)
Rép.: (coussin SAUF (divan OU table)) OU (table SAUF (coussin OU divan)) OU (coussin ET divan)
Preuve: L’arbre renversé de la requête donnée en réponse est:
Si on remplace chaque noeud par le diagramme de Venn correspondant, on obtient (cliquez sur l’image pour une version plus grande):
Le diagramme final de la requête (le plus à droite) correspond bien au diagramme de la question.
Rép.: ((table SAUF coussin) SAUF divan) OU (coussin ET divan)